Cryptographic Keys

In the XAG Ledger, a digital signature proves that a transaction is authorized to do a specific set of actions. Only signed transactions can be submitted to the network and included in a validated ledger.

Every digital signature is based on a cryptographic key pair associated with the transaction's sending account. A key pair may be generated using any of the XAG Ledger's supported cryptographic signing algorithms. A key pair can be used as a master key pair, regular key pair or a member of a signer list, regardless of what algorithm was used to generate it.

Warning: It is important to maintain proper security over your secret keys. Digital signatures are the only way of verifying to the XAG Ledger that you are authorized to send a transaction, and there is no privileged administrator who can undo or reverse any transaction that has been applied to the ledger. If someone else knows the secret key of your XAG Ledger account, that person can create digital signatures to authorize any transaction the same as you could.

Generating Keys

You generate a key pair using the wallet_propose method. Here's a sample wallet_propose response:

{
  "result": {
    "account_id": "rDGnaDqJczDAjrKHKdhGRJh2G7zJfZhj5q",
    "key_type": "secp256k1",
    "master_key": "COON WARN AWE LUCK TILE WIRE ELI SNUG TO COVE SHAM NAT",
    "master_seed": "sstV9YX8k7yTRzxkRFAHmX7EVqMfX",
    "master_seed_hex": "559EDD35041D3C11F9BBCED912F4DE6A",
    "public_key": "aBQXEw1vZD3guCX3rHL8qy8ooDomdFuxZcWrbRZKZjdDkUoUjGVS",
    "public_key_hex": "0351BDFB30E7924993C625687AE6127034C4A5EBA78A01E9C58B0C46E04E3A4948"
  },
  "status": "success",
  "type": "response"
}

The response contains a key pair (a seed and a public key, in various formats) as well as an account_id.

Seed

A seed value is a compact value that is used to derive the actual secret key (and public key) for an account. The master_key, master_seed, and master_seed_hex all represent the same seed value, in various formats. Any of these formats can be used to sign transactions in the rippled APIs and some other XAGL software. Despite being prefixed with master_, the keys this seed represents are not necessarily the master keys for an account; you can use a key pair as a regular key or a member of a multi-signing list as well.

Because the seed value is the basis for all the other information of an account, you must protect it very carefully. Anyone who has knows an address's seed value effectively has full control over that address.

Secret Key

The wallet_propose response does not explicitly list the secret key value, also called a private key. Software that can sign transactions is expected to derive the secret key from the seed value.

Public Key

The public_key and public_key_hex both represent the same public key value. The public key is derived from the secret key as part of key derivation. The public key makes it possible to verify the authenticity of a transaction signature, but not to create more signatures.

account_id

The account_id is derived from the public key and designates the potential for an account to be created in the XAG Ledger. It is important to know that while an account_id exists, no actual account exists in the XAG Ledger until the account_id receives its first XAG payment. In addition, the account_id can't send any transactions until after it's received a transaction that funds and creates the account.

The account_id (without a funded account) can, however, be used as a regular key or a member of a signer list to authorize transactions for another account that does exist.

To create a funded account stored in the ledger, the account_id must receive a Payment transaction that provides enough XAG to meet the reserve requirement.

For more information about the wallet_propose response, see wallet_propose.

You can use this generated key pair in one of three ways: as a master key pair, regular key pair, or signer list member.

Key Type

The field key_type indicates what cryptographic signing algorithm was used to generate this key pair. You can specify the key_type when you make the request to generate a key pair using the wallet_propose method.

Master Key Pair

The master key pair is composed of a secret key and a public key. In addition to being able to sign all transactions that a regular key pair can, the master key pair's secret key is the only key that can be used to perform the following actions:

• Disable the master public key.

• Permanently give up the ability to freeze.

• Send a cost-0 key reset transaction.

The master key pair for an account is generated in the same wallet_propose response as the account_id of the account the master key pair is authorized to sign transactions for. Because the master key pair is generated in the same response, it is intrinsically related to the address, which is derived from the public key.

This is as opposed to a regular key pair, which is also generated using the wallet_propose method, but which must be explicitly assigned as a regular key pair to an account. Because a regular key pair is explicitly assigned, it is not intrinsically related to the address of the account it is authorized to sign transactions for. For more information, see Regular Key Pair.

Caution: A master key pair cannot be changed, but it can be disabled. This means that if your master seed or secret key is compromised, rather than change it, you must disable it.

Because a master key pair cannot be changed and can only be disabled in the event of a compromise, this is a compelling reason to keep your master key pair offline and set up a regular key pair to sign transactions from your account instead.

Keeping your master key pair offline means not putting your master secret key anywhere that malicious actors can get access to it. For example, this can mean keeping it on an air-gapped machine that never connects to the internet, on a piece of paper stored in a safe, or in general, not within reach of a computer program that interacts with the internet at large. Ideally, a master key pair is used only on the most trusted of devices and for emergencies only, such as to change a regular key pair in the event of a possible or actual compromise.

Regular Key Pair

The XAG Ledger allows an account to authorize a secondary key pair, called a regular key pair, to sign future transactions, while keeping your master key pair offline. If the seed or secret key of a regular key pair is compromised, you can remove or replace the key pair without changing the rest of your account. This saves the trouble of re-establishing the account's settings and relationships to other accounts. You can also rotate a regular key pair proactively. (Neither of those things is possible for the master key pair of an account, which is intrinsically linked to the account's address.)

You generate a key pair to use as a regular key pair using the wallet_propose method. However, unlike with a master key pair, which is generated alongside and intrinsically related to the account_id of an account it supports, you must explicitly create the relationship between a regular key pair and the account you want it to sign transactions for. You use the SetRegularKey method to assign a regular key pair to an account.

For a tutorial on assigning a regular key pair, see Assign a Regular Key Pair.

After you assign a regular key pair to an account, the account has two key pairs associated with it:

• A master key pair that is intrinsically related to the account's account_id and which you should keep offline.
• A regular key pair that you've explicitly assigned to the account and which you use to sign transactions for the account.

You can assign one regular key pair to an account and use it to sign all transactions, except for the ones reserved for the master key pair.

You can remove or change a regular key pair at any time. This means that if a regular secret key is compromised (but the master secret key is not), you can regain control of your account by simply removing or changing the regular key pair.

For a tutorial on changing or removing a regular key pair, see Assign a Regular Key Pair.

Signing Algorithms

Cryptographic key pairs are always tied to a specific signing algorithm, which defines the mathematical relationships between the secret key and the public key. Cryptographic signing algorithms have the property that, given the current state of cryptographic techniques, it is "easy" to use a secret key to calculate a matching public key, but it is effectively impossible to compute a matching secret key by starting from a public key.

The XAG Ledger supports the following cryptographic signing algorithms:

Key Type	Algorithm	Description
secp256k1	ECDSA using the elliptic curve secp256k1	This is the scheme used in Bitcoin. The XAG Ledger uses these key types by default.
ed25519	EdDSA using the elliptic curve Ed25519	This is a newer algorithm which has better performance and other convenient properties. Since Ed25519 public keys are one byte shorter than secp256k1 keys, rippled prefixes Ed25519 public keys with the byte 0xED so both types of public key are 33 bytes.

When you generate a key pair with the wallet_propose method, you can specify the key_type to choose which cryptographic signing algorithm to use to derive the keys. If you generated a key type other than the default, you must also specify the key_type when signing transactions.

The supported types of key pairs can be used interchangeably throughout the XAG Ledger as master key pairs, regular key pairs, and members of signer lists. The process of deriving an address is the same for secp256k1 and Ed25519 key pairs.

Future Algorithms

In the future, it is likely that the XAG Ledger will need new cryptographic signing algorithms to keep up with developments in cryptography. For example, if quantum computers using Shor's algorithm (or something similar) will soon be practical enough to break elliptic curve cryptography, XAG Ledger developers can add a cryptographic signing algorithm that isn't easily broken. As of early 2020, there's no clear first choice "quantum-resistant" signing algorithm and quantum computers are not yet practical enough to be a threat, so there are no immediate plans to add any specific algorithms.

Key Derivation

The process of deriving a key pair depends on the signing algorithm. In all cases, keys are generated from a seed value that is 16 bytes (128 bits) in length. The seed value can be completely random (recommended) or it can be derived from a specific passphrase by taking the SHA-512 hash and keeping the first 16 bytes (similar to SHA-512Half, but keeping only 128 bits instead of 256 bits of the output).

Sample Code

The key derivation processes described here are implemented in multiple places and programming languages:

• In C++ in the rippled code base:
  • Seed definition
  • General & Ed25519 key derivation
  • secp256k1 key derivation
• In Python 3 in this repository's code samples section .
• In JavaScript in the ripple-keypairs package.

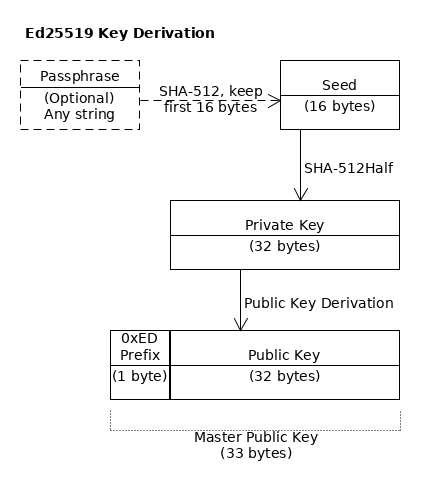
Ed25519 Key Derivation

[Source]

1. Calculate the SHA-512Half of the seed value. The result is the 32-byte secret key.

   Tip: All 32-byte numbers are valid Ed25519 secret keys. However, only numbers that are chosen randomly enough are secure enough to be used as secret keys.

2. To calculate an Ed25519 public key, use the standard public key derivation for Ed25519 to derive the 32-byte public key.

   Caution: As always with cryptographic algorithms, use a standard, well-known, publicly-audited implementation whenever possible. For example, OpenSSL has implementations of core Ed25519 and secp256k1 functions.

3. Prefix the 32-byte public key with the single byte 0xED to indicate an Ed25519 public key, resulting in 33 bytes.

   If you are implementing code to sign transactions, remove the 0xED prefix and use the 32-byte key for the actual signing process.

4. When serializing an account public key to base58, use the account public key prefix 0x23.

   Validator ephemeral keys cannot be Ed25519.

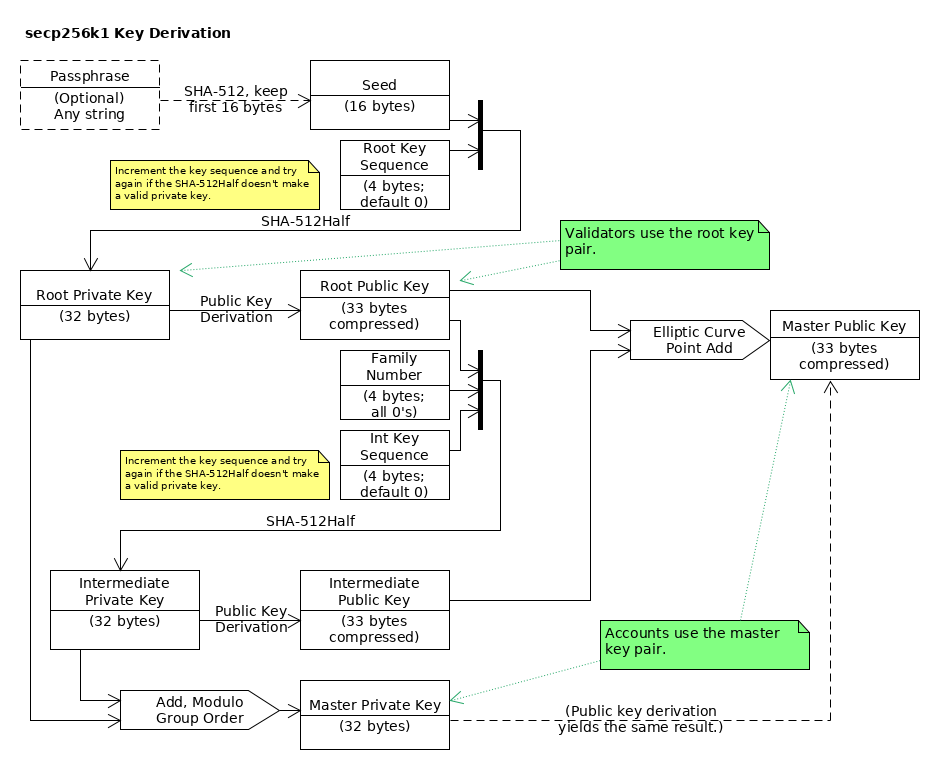
secp256k1 Key Derivation

[Source]

Key derivation for secp256k1 XAG Ledger account keys involves more steps than Ed25519 key derivation for a couple reasons:

• Not all 32-byte numbers are valid secp256k1 secret keys.
• The XAG Ledger's reference implementation has an unused, incomplete framework for deriving a family of key pairs from a single seed value.

The steps to derive the XAG Ledger's secp256k1 account key pair from a seed value are as follows:

1. Calculate a "root key pair" from the seed value, as follows:

   1. Concatenate the following in order, for a total of 20 bytes:

      • The seed value (16 bytes)
      • A "root sequence" value (4 bytes), as a big-endian unsigned integer. Use 0 as a starting value for the root sequence.

   2. Calculate the SHA-512Half of the concatenated (seed+root sequence) value.

   3. If the result is not a valid secp265k1 secret key, increment the root sequence by 1 and start over. [Source]

      A valid secp256k1 key must not be zero, and it must be numerically less than the secp256k1 group order. The secp256k1 group order is the constant value 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141.

   4. With a valid secp256k1 secret key, use the standard ECDSA public key derivation with the secp256k1 curve to derive the root public key. (As always with cryptographic algorithms, use a standard, well-known, publicly-audited implementation whenever possible. For example, OpenSSL has implementations of core Ed25519 and secp256k1 functions.)

   Tip: Validators use this root key pair. If you are calculating a validator's key pair, you can stop here. To distinguish between these two different types of public keys, the base58 serialization for validator public keys uses the prefix 0x1c.

2. Convert the root public key to its 33-byte compressed form.

   The uncompressed form of any ECDSA public key consists of a pair of 32-byte integers: an X coordinate, and a Y coordinate. The compressed form is just the X coordinate and a one-byte prefix: 0x02 if the Y coordinate is even, or 0x03 if the Y coordinate is odd.

   You can convert an uncompressed public key to the compressed form with the openssl commandline tool. For example, if the uncompressed public key is in the file ec-pub.pem, you can output the compressed form like this:

   $ openssl ec -in ec-pub.pem -pubin -text -noout -conv_form compressed
   

3. Derive an "intermediate key pair" from the compressed root public key you, as follows:

   1. Concatenate the following in order, for a total of 41 bytes:

      • The compressed root public key (33 bytes)
      • 0x00000000000000000000000000000000 (4 bytes of zeroes). (This value was intended to be used to derive different members of the same family, but in practice only the value 0 is used.)
      • A "key sequence" value (4 bytes), as a big-endian unsigned integer. Use 0 as a starting value for the key sequence.

   2. Calculate the SHA-512Half of the concatenated value.

   3. If the result is not a valid secp265k1 secret key, increment the key sequence by 1 and restart deriving the account's intermediate key pair.

   4. With a valid secp256k1 secret key, use the standard ECDSA public key derivation with the secp256k1 curve to derive the intermediate public key. (As always with cryptographic algorithms, use a standard, well-known, publicly-audited implementation whenever possible. For example, OpenSSL has implementations of core Ed25519 and secp256k1 functions.)

4. Derive the master public key pair by adding the intermediate public key to the root public key. Similarly, derive the secret key by adding the intermediate secret key to the root secret key.

   • An ECDSA secret key is just a very large integer, so you can calculate the sum of two secret keys by summing them modulo the secp256k1 group order.

   • An ECDSA public key is a point on the elliptic curve, so you should use elliptic curve math to sum the points.

5. Convert the master public key to its 33-byte compressed form, as before.

6. When serializing an account's public key to its base58 format, use the account public key prefix, 0x23.

   See Address Encoding for information and sample code to convert from an account's public key to its address.